semana 4

Curvas circulares

Las curvas horizontales circulares simples son arcos de circunferencia de un solo radio que unen dos tangentes consecutivas, conformando la proyección horizontal de las curvas reales o espaciales.

Elementos de la curva circular

P.C. : Punto de inicio de la curva 

P.I. : Punto de Intersección de 2 alineaciones consecutivas 

P.T. : Punto de tangencia 

E : Distancia a externa (m) 

M : Distancia de la ordenada media (m) 

R : Longitud del radio de la curva (m) 

T : Longitud de la subtangente (P.C a P.I. y P.I. a P.T.) (m) 

L : Longitud de la curva (m) 

L.C : Longitud de la cuerda (m)

∆ : Ángulo de deflexión (º) 

p : Peralte; valor máximo de la inclinación transversal de la calzada, asociado al diseño de la curva (%) 

Sa : Sobreancho que pueden requerir las curvas para compensar el aumento de espacio lateral que experimentan los vehículos al describir la curva (m) 

Nota: Las medidas angulares se expresan en grados sexagesimales. 

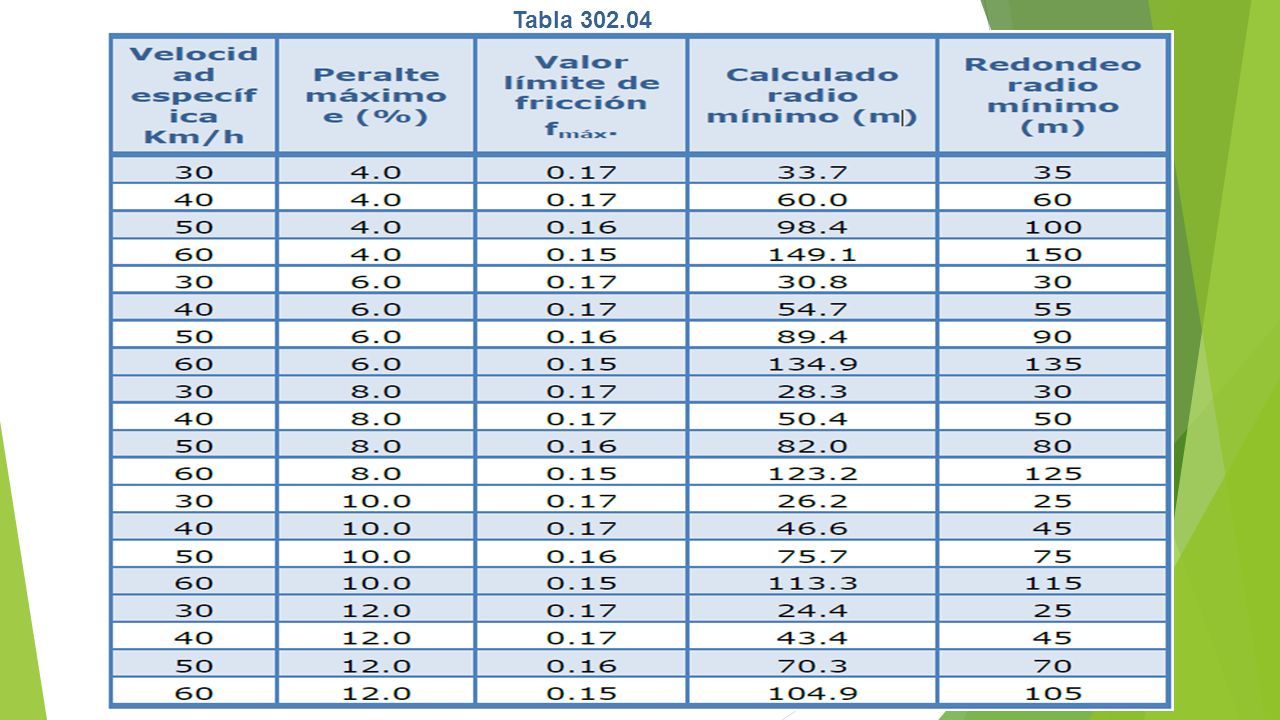
Radios mínimos 

Los radios mínimos de curvatura horizontal son los menores radios que pueden recorrerse con la velocidad de diseño y la tasa máxima de peralte, en condiciones aceptables de seguridad y comodidad, para cuyo cálculo puede utilizarse la siguiente fórmula: 

                𝑅𝑚í𝑛 = 𝑉 2 /127(𝑃𝑚á𝑥 + 𝑓𝑚á𝑥. ) 

Dónde: 

Rmín : Radio Mínimo 

V : Velocidad de diseño 

Pmáx: Peralte máximo asociado a V (en tanto por uno). 

ƒmáx: Coeficiente de fricción transversal máximo asociado a V. 

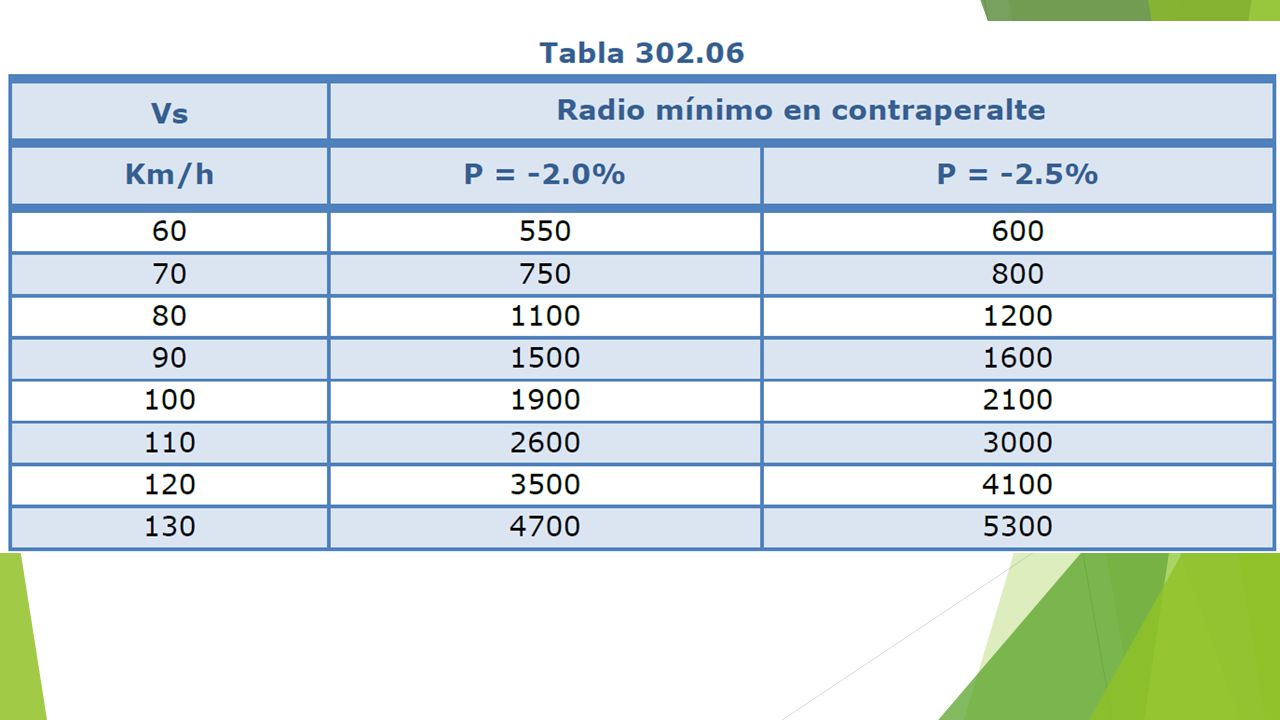
Curvas en contraperalte

Sobre ciertos valores del radio, es posible mantener el bombeo normal de la vía, resultando una curva que presenta, en uno o en todos sus carriles, un contraperalte en relación al sentido de giro de la curva. Puede resultar conveniente adoptar esta solución cuando el radio de la curva es igual o mayor que el indicado, en alguna de las siguientes situaciones: 

• La pendiente longitudinal es muy baja y la transición de peralte agudizará el problema de drenaje de la vía.
• Se desea evitar el escurrimiento de agua hacia el separador central. 
• En zonas de transición dónde existen ramales de salida o entrada asociados a una curva amplia de la carretera, se evita el quiebre de la arista común entre ellas. 

El criterio empleado para establecer los radios límites que permiten el uso del contraperalte se basa en: 

• Bombeo considerado = -2.5% 
• Coeficiente de fricción lateral aceptable ƒ = ƒmáx/2 Por lo tanto:

               𝑅 𝑙í𝑚𝑖𝑡𝑒 𝑐𝑜𝑛𝑡𝑟𝑎𝑝𝑒𝑟𝑎𝑙𝑡𝑒 = 𝑉 2 /127 ( ƒ𝑚á𝑥/2 − 0.025)

Para velocidades menores a 80 km/h, el radio mínimo con contraperalte se elevó sustancialmente en prevención de velocidades de operación muy superiores a las de diseño. Para las demás velocidades esta eventualidad está ampliamente cubierta por el factor de seguridad aplicado al factor "ƒmáx". 

En sectores singulares del trazo, tales como transiciones de dos vías a una vía, o bien, dónde se deba modificar el ancho de la mediana para crear carriles auxiliares de tránsito rápido, situaciones que deberán señalizarse con la debida anticipación y con indicación de la velocidad máxima aceptable, se podrán diseñar curvas en contraperalte, pero en ese caso se respetarán los radios iguales o mayores que los especificados 

Transición de peralte

Siendo el peralte la inclinación transversal de la carretera en los tramos de curva, destinada a contrarrestar la fuerza centrífuga del vehículo, la transición de peralte viene a ser la traza del borde de la calzada, en la que se desarrolla el cambio gradual de la pendiente de dicho borde, entre la que corresponde a la zona en tangente, y la que corresponde a la zona peraltada de la curva.

Para efectos de la presente norma, el peralte máximo se calcula con la siguiente fórmula:

                   𝑖𝑝𝑚á𝑥 = 1.8 −0.01 𝑉 

Dónde: 

ipmáx : Máxima inclinación de cualquier borde de la calzada respecto al eje de la vía (%). 

V : Velocidad de diseño (km/h).

La longitud del tramo de transición del peralte tendrá por tanto una longitud mínima definida por la fórmula: 

                

    𝐿𝑚í𝑛 = 𝑝𝑓− 𝑝𝑖 / 𝑖𝑝𝑚á𝑥=B

Dónde: 

Lmín : Longitud mínima del tramo de transición del peralte (m).    pf : Peralte final con su signo (%) 

 pi : Peralte inicial con su signo (%) 

B : Distancia del borde de la calzada al eje de giro del peralte (m).

La transición del peralte deberá llevarse a cabo combinando las tres condiciones siguientes: 

• Características dinámicas aceptables para el vehículo 
• Rápida evacuación de las aguas de la calzada. 
• Sensación estética agradable.

Sobreancho

Es el ancho adicional de la superficie de rodadura de la vía, en los tramos en curva para compensar el mayor espacio requerido por los vehículos.

Necesidad del sobreancho

La necesidad de proporcionar sobreancho en una calzada, se debe a la extensión de la trayectoria de los vehículos y a la mayor dificultad en mantener el vehículo dentro del carril en tramos curvos.

En curvas de radio pequeño y mediano, según sea el tipo de vehículos que circulan habitualmente por la carretera, ésta debe tener un sobreancho con el objeto de asegurar espacios libres adecuados (holguras), entre vehículos que se cruzan en calzadas bidireccionales o que se adelantan en calzadas unidireccionales, y entre los vehículos y los bordes de las calzadas. El sobreancho requerido equivale al aumento del espacio ocupado transversalmente por los vehículos al describir las curvas más las holguras teóricas adoptadas (valores medios). El sobreancho no podrá darse a costa de una disminución del ancho de la berma.

Desarrollo del sobreancho

Con el fin de disponer de un alineamiento continuo en los bordes de la calzada, el sobreancho debe desarrollarse gradualmente a la entrada y salida de las curvas. 

En el caso de curvas circulares simples, por razones de apariencia, el sobreancho se debe desarrollar linealmente a lo largo del lado interno de la calzada, en la misma longitud utilizada para la transición del peralte. En las curvas con espiral, el sobreancho se desarrolla linealmente, en la longitud de la espiral.

 Normalmente la longitud para desarrollar el sobreancho será de 40 m. Si la curva de transición es mayor o igual a 40 m, el inicio de la transición se ubicará 40 m, antes del principio de la curva circular. Si la curva de transición es menor de 40 m, el desarrollo del sobreancho se ejecutará en la longitud de la curva de transición disponible. Para la determinación del desarrollo del sobreancho se utilizará la siguiente fórmula: 

                       𝑆𝑎𝑛 = 𝑆𝑎 / 𝐿= 𝑙n

Dónde: 

San : Sobreancho correspondiente a un punto distante ln metros desde el origen. 

L : Longitud total del desarrollo del sobreancho, dentro de la curva de transición. 

ln : Longitud en cualquier punto de la curva, medido desde su origen (m).

La ordenada San se medirá normal al eje de la calzada en el punto de abscisa ln y el borde de la calzada ensanchada distará del eje a/2+ San siendo "a" el ancho normal de la calzada en recta. 

La demarcación de la calzada se ejecutará midiendo una ordenada San /2, a partir del eje de la calzada, en el punto de la abscisa ln.

Longitud de transición y desarrollo del sobreancho

la repartición del sobreancho se hace en forma lineal empleando para ello, la longitud de transición de peralte, de esta forma se puede conocer el sobreancho deseado en cualquier punto, usando la siguiente fórmula. 

                  𝑆𝑎𝑛 = 𝑆𝑎 / 𝐿=𝐿𝑛 

Dónde: 

San : Sobreancho deseado en cualquier punto (m) 

Sa : Sobreancho calculado para la curva, (m) 

Ln : Longitud a la cual se desea determinar el sobreancho (m) 

L : Longitud de transición de peralte (m). 

La distribución del sobreancho cuando un arco de espiral empalma dos arcos circulares de radio diferente y del mismo sentido, se debe hacer aplicando la siguiente fórmula, la cual se obtiene a partir de una distribución lineal. 

Verificación de la distancia de visibilidad

La coordinación de los alineamientos horizontal y vertical, respecto a las distancias de visibilidad, debe efectuarse al inicio del proyecto, es decir cuando aún es posible hacer modificaciones en el diseño.

Dicho valor puede ser calculado analíticamente mediante la fórmula siguiente:

      𝑎𝑚á𝑥 = 𝐷𝑣2 / 8𝑅 

Con dicha fórmula se obtienen resultados aproximados para todos los efectos, cuando se calcula amáx por condición de parada o cuando se calcula amáx para R > Da en el caso de visibilidad de adelantamiento. 

Si la verificación indica que no se tiene la distancia de visibilidad requerida y no es posible aumentar el radio de la curva, se deberá recurrir al método gráfico para calcular las rectificaciones necesarias, ya sea que se trate de un talud de corte u otro obstáculo que se desarrolla a lo largo de toda o parte de la curva.